Pearcey integral
From HandWiki
Short description: Class of canonical diffraction integrals
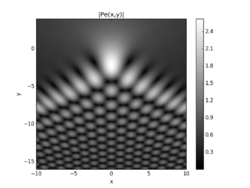

In mathematics, the Pearcey integral is defined as[1]
The Pearcey integral is a class of canonical diffraction integrals, often used in wave propagation and optical diffraction problems[2] The first numerical evaluation of this integral was performed by Trevor Pearcey using the quadrature formula.[3][4]

In optics, the Pearcey integral can be used to model diffraction effects at a cusp caustic, which corresponds to the boundary between two regions of geometric optics: on one side, each point is contained in three light rays; on the other side, each point is contained in one light ray.
References
- ↑ Frank W. J. Olver, Daniel W. Lozier, Ronald F. Boisvert, Charles W. Clark, NIST Handbook of Mathematical Functions, p. 777, Cambridge, 2010
- ↑ Paris, R. B. (2011). Hadamard Expansions and Hyperasymptotic Evaluation. doi:10.1017/CBO9780511753626. ISBN 9781107002586. https://books.google.com/books?id=8WggWK8AecIC&pg=PA207.
- ↑ Pearcey, T. (1946). "XXXI. The structure of an electromagnetic field in the neighbourhood of a cusp of a caustic". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 37 (268): 311–317. doi:10.1080/14786444608561335.
- ↑ López, José L.; Pagola, Pedro J. (2016). "Analytic formulas for the evaluation of the Pearcey integral". Mathematics of Computation 86 (307): 2399–2407. doi:10.1090/mcom/3164.
 |
